JUTANT Ludovic
GTR 1
Groupe H
TP MUPAD n°1
EXERCICES
Exercice 1 :
·expand((x^2+y)^5)
5 10 8 2 4 4 3 6 2
y + x + 5 x y + 5 x y + 10 x y + 10 x y
Exercice 2 :
·simplify((x^2-1)/(x+1))
x - 1
Exercice 3 :

Exercice 4 :
1°)
·limit(sin(x)/x, x =0) = 1
2°)
·limit((1-cos(x)/x,x=0) = 0
3°)
·limit(ln(x),x=+0) = -infinity
4°)
·limit(x^(sin(x)),x=0) = 1
5°)
·limit((1+(1/x))^x,x=+infinity) = exp(1)
6°)
·limit((1+((ln (2))/x))^x,x=+infinity) = 2
7°)
·limit(2/(1+exp(-1/x)),x=0 , Left) = 0
Sup :
·limit((sin(x))^(1/x),x=0) = undefined
Exercice 5
·f:=((x^3-3*x+2)/(x+1))
·discont(f,x)
{-1}
·Limite à gauche de f(x) : limit(f,x=-1,Left) = -infinity
·Limite à droite de f(x) : limit(f,x=-1,Right) = infinity
·Limite en moins l'infini :limit(f,x=-infinity) = infinity
·Limite en plus l'infini :limit(f,x=infinity) = infinity
·Calcul de la dérivé : D(f)
3 x² D(x) - 3 D(x) D(x) (x^3 - 3 x + 2)
------------------ - -------------------
x + 1 (x + 1)²
Mais pour ne pas avoir de terme qui ne serve a rien comme D(x) on fait :
·diff(f,x)
3 x² - 3 x^3 - 3 x + 2
-------- - ------------
x + 1 (x + 1)²
·Je pose g = f'(x) => g:=diff(f,x)
3 x² - 3 x^3 - 3 x + 2
-------- - ------------
x + 1 (x + 1)²
·Je résouds g(x)=0 => solve(g=0,x)
1/2 1/2
{1, - 1/4 I 15 - 5/4, 1/4 I 15 - 5/4}
· f’’(x) = diff(g,x)
6 x 2 (3 x² - 3) 2 (x^3 - 3 x + 2)
----- - ------------ + ----------------
x + 1 (x + 1)² (x + 1)^3
d = f’’
·On met tout sur le meme dénominateur : factor(d)
2 (3 x + 3 x² + x^3 + 5)
--------------------------
(x + 1)^3
Comme la factorisation de f’’nous donne que des nombres positif, il est facile de remarquer que le numérateur sera positif pour quelque soit x positif donc f’’(1) est différent de 0. Par conséquent 1 n’est pas un extremum .
·asympt(f,x)
2 4 4 / 1 \
x - x - 2 + - - -- + O | -- |
x x² 2 \ x^3/
Exercice 6 :
Décomposition en éléments simple, calcul d'intégrale
1°) F:=(4*x^6 + 8*x^5 - 5*x^4 - 9*x^3 - 4*x^2 + 22*x -32)/(x^7 + 3*x^6 - 4*x^5 - 2*x^4 + 18*x^3 - 28*x^2 + 21*x - 9 )
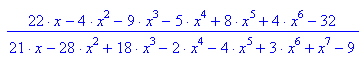
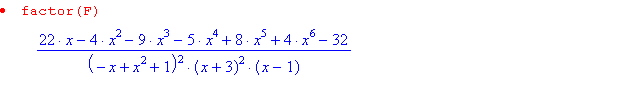
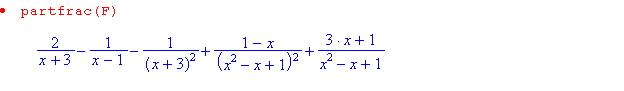
2°)primitives :
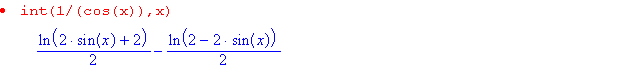


Exercice 7 :
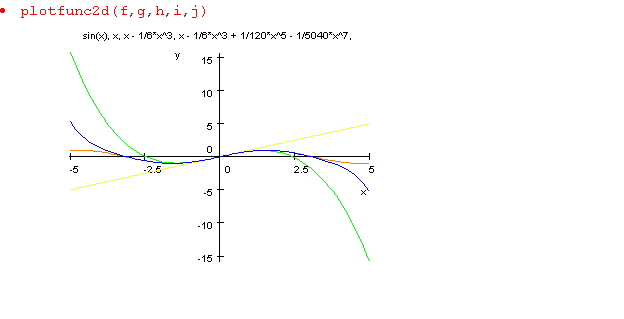
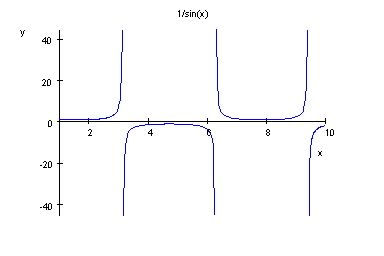
Tracer de courbes :